Object recognition by convolutional neural network for multiple classes using lambda processes

Shamuratov Oleksii.

Lviv Polytechnic National University

Lviv, Ukraine

Abstract: The developed architecture of a convolutional artificial neural network for object search is considered in the work. A feature of the development is the use of lambda architecture and saving neural network states in the data warehouse, which allows you to run the process of finding objects in the image in parallel for each class stored in the data warehouse. The paper presents the developed topology of the convolutional network and the components of the architecture used to run parallel processes.

Keywords: convolutional neural networks, object search, lambda architecture, parallel calculations.

Introduction

In today’s world, the online entertainment industry is growing rapidly, creating demand for better products. This in turn has led to the use of artificial intelligence not only in science but also in entertainment. Programs that allow you to change objects in images are gaining popularity. This entails the problem of defining different classes of objects in the image. This paper presents an approach to solving the problem of the dynamic number of classes for recognition by an artificial neural network.

Literature review

Artificial neural networks are one of the most effective and common ways to represent and solve image recognition problems. Neural networks perform very well in pattern recognition problems because it combines mathematical and logical calculations. The neural network allows you to process many factors, regardless of their origin, this is a stable universal algorithm. Neural networks allow to build dependencies of parameters in the form of a polynomial based on educational sample that very simplifies realization of recognition of objects ^[1].

General mathematical model of the neuron (Fig. 1):

• x_i input signals coming from the environment or from other active neurons. Input levels can be discrete from sets [0, 1] or [-1, 1] or take any real value.
• weights w_i – determine the strength of the connection between neurons.
• level of activation of the neuron P = ∑ w_ix_i.
• activation function Y=f(P) is used to calculate the output value of the signal transmitted to other neurons ^[2].

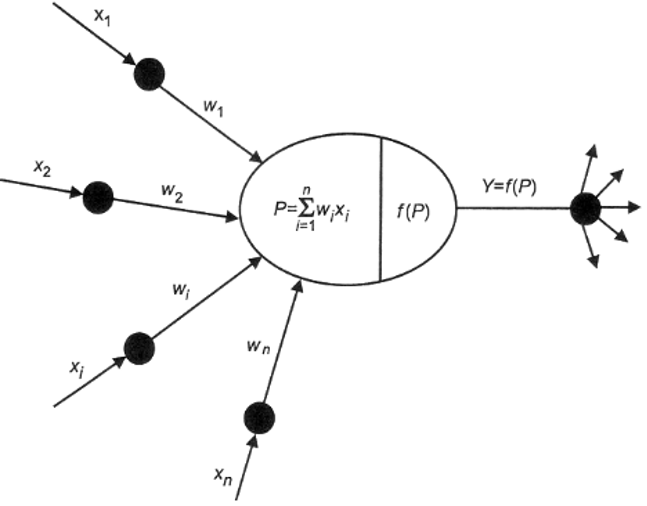
The input signals x_i are multiplied by the weights w_i (synaptic weights), and the resulting weighted sum

 is changed by the function f(P) (activation function). The input signal Y can also be weighed (scaled). Different functions are used as the activation function, but more often the sigmoid function

  (Fig. 2), as well as the hyperbolic tangent, logarithmic function, linear and others. The main requirement for such functions is monotony ^[3].

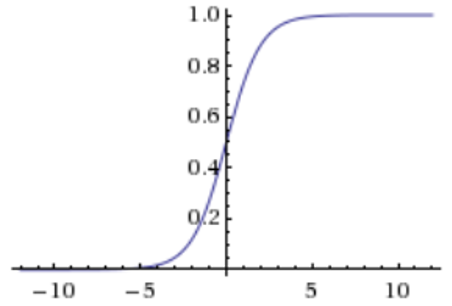
One of the factors why sigmoid is used in neural networks is the simple expression of its derivative through the function S`(x)=S(x)·(1-S(x)), which significantly reduces the computational difficulty of the method of inverse error distribution. The neural network implements a simple regression model for N independent variables. If you combine many neurons into neural structures, the function you perform can be as complex as you like. A neural network is a set of computing elements (neurons), each of which has several synapse inputs and one axon output ^[4].

Materials and Methods

Convolutional neural networks provide partial resistance to changes in scale, shifts, rotations, changes in angle and other distortions. Convolutional neural networks combine three architectural ideas to provide invariance to scale change, shift rotation and spatial distortion:

• local receptor fields.
• general synaptic coefficients.
• hierarchical organization with spatial sub-samples.

Currently, the convolutional neural network and its modifications are considered the best in accuracy and speed of algorithms for finding objects in the image ^[5].

Let us consider in more detail the topology of the convolutional neural network (Fig. 2), which will be used to search for objects.

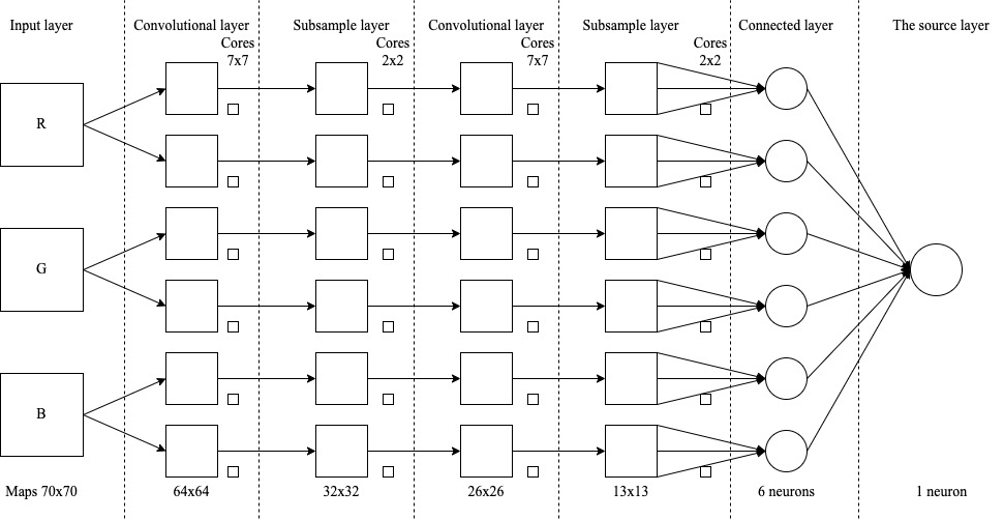
The input will be raster images with a size of 70×70 pixels. With the larger dimension, the computational complexity increased greatly, so these parameters are the best in the format of computing capacity and recognition accuracy. The image is divided into three RGB channels, so the input layer has 3 maps the size of the input image ^[6]. The input data are normalized in the range [0, 1] by the formula:

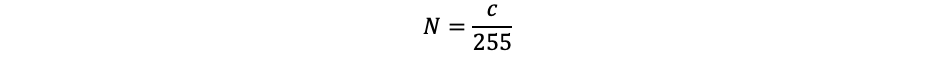
c is the value of the channel of a particular pixel ^[7].

The convolutional layer consists of 6 maps measuring 64×64, each map contains a synaptic core measuring 7×7. More maps will increase the recognition accuracy by about 5%, but this is a bad aspect of increasing the capacitive complexity of calculations by 40% compared to the chosen topology. By choosing a smaller dimension for the cores, the neural network misses some important features of objects, which significantly reduced the accuracy of recognition ^[8]. Therefore, it was decided that these parameters will be optimal for the algorithm. The dimensions of the maps were calculated by the formula:

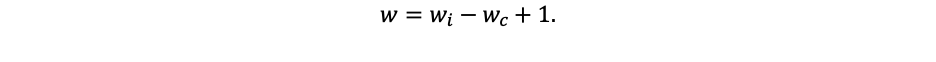
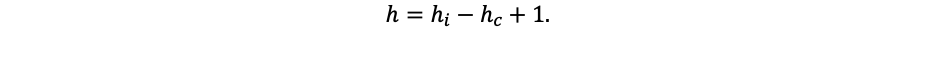
• w_i, h_i – width and height of the map of the previous layer.
• w_c, h_c – width and height of the core of the current layer.

At the beginning of each map of the convolutional layer is equal to 0. The values of the weights of the cores are set randomly from the range [-0.5, 0.5]. Coagulation will be carried out according to the formula:

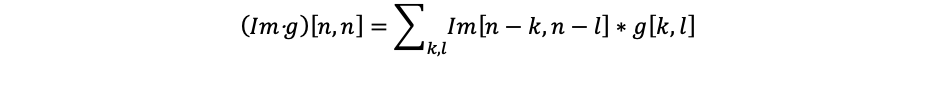
• Im is the matrix of the input image.
• g is the convolution core.
• n – i s the dimension.
• k, l are the specific values in the matrix at the cycle step.

The method of processing the edges of the image was chosen to approach the larger size of the matrix, which will provide a better analysis of the features of objects and the edges of the image. Then the final convolution formula, considering the selected activation function of the hyperbolic tangent, will take the form:

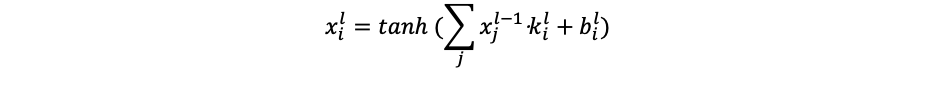
• x_i^l is the map of features and the source layer l.
• b^l is the shear coefficient of layer l for the feature map i.
• k_i^l is the core of the convolution of layer l for the feature map i.

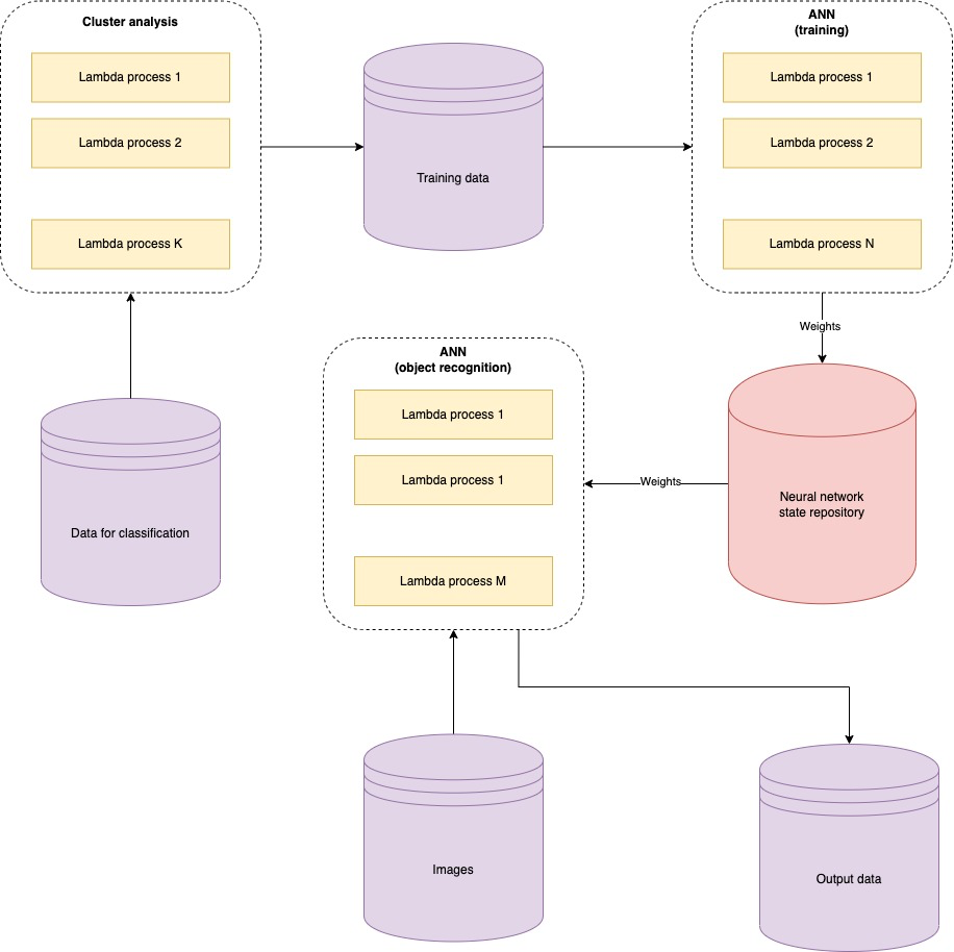
The RelU function was chosen to form the features of the subsample. The source layer should consist of the number of neurons, which corresponds to the number of classes of objects that will be analyzed by the neural network ^[9]. However, in our system, object classes are added dynamically and will increase over time. This raises the problem of scaling the artificial neural network algorithm, so it was decided to use the lambda architecture for the neural network algorithm (Fig. 3). And store the obtained weights for each class of objects in the database. This approach will allow the output of only one neuron, which will characterize the belonging of the object to a certain class. The neural network algorithm itself will run separate processes for each object class and retrieve the required weights from the data warehouse, which will easily scale the neural network and reduce the computational complexity of network learning because it will require running processes equal to the number of input image classes.

Conclusions

An architecture of a convolutional neural network has been developed, which would ensure stable operation for objects recognition in images and adhere to the concept of lambda-architectural approach. The activation function used the hyperbolic tangent. The neural network structure has 2 convolutional layers, 2 subsample layers and one fully connected layer. This made it possible to process objects with resistance to rotation or scaling of the object, changing the angle without the need to re-analyze them. It also made it possible to save the analyzed objects in a database without the need to reprocess them.

References

[1] Sibt ul Hussain, “Machine Learning Methods for Visual Object Detection”. p. 160, 2012.

[2] Bartfai G.A. Comparison of Two ART-base Neural Networks for Hierarchical Clustering // ANNES’95, The Second New Zealand International Two-Stream Conference On Artifical Neural Networks and Expert Systems, IEEE Computer Society Press, 1995.–P.83-86.

[3] Carpenter G.A., Grossberg S., Markuzon N., Reynolds J.H., Rosen D.B. Fuzzy ARTMAP: A neural network architecture for incremental supervised learning of analog multidimensional maps // IEEE Trans. Neural Networks, 1992.–vol.3.–P.698-713.

[4] Peleshko, Dmytro, et al. “Design and implementation of visitors queue density analysis and registration method for retail videosurveillance purposes.” 2016 IEEE First International Conference on Data Stream Mining & Processing (DSMP). IEEE, 2016.

[5] Simard P., David S., John C. Platt. «Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis.» In ICDAR, vol. 3, pp. 958—962. 2003.

[6] Zeiler, M., Krishnan, D., Taylor, G., Fergus, R. Deconvolutional networks. In CVPR. 2010.

[7] Szegedy Christian, Liu Wei, Jia Yangqing, Sermanet Pierre, Reed Scott E., Anguelov Dragomir, Erhan Dumitru, Vanhoucke Vincent, Rabinovich Andrew. «Going deeper with convolutions». IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2015, Boston, MA, USA, June 7–12, 2015. IEEE Computer Society. pp. 1–9.

[8] Valueva M.V., Nagornov N.N., Lyakhov P.A., Valuev G.V., Chervyakov N.I. “Application of the residue number system to reduce hardware costs of the convolutional neural network implementation”. Mathematics and Computers in Simulation. Elsevier BV. 2020.

[9] Romanuke Vadim. Appropriate number and allocation of ReLUs in convolutional neural networks. Research Bulletin of NTUU “Kyiv Polytechnic Institute” : journal. — 2017. — Vol. 1. — P. 69—78